CIENTÍFICO N1
NOTA DEL TUTOR PARA EL III TRIMESTRE:
INTRODUCCIÓN.
CONCEPTO DE ECUACIÓN
Antes de empezar con
la resolución de ecuaciones de primer grado propiamente dicha,
vamos a ver un poco qué es una ecuación.
Una ecuación es una igualdad algebraica que se cumple
solamente para determinados valores de las variables o incógnitas (las letras). Por ejemplo, la siguiente
igualdad algebraica es una ecuación:
7x – 3 = 3x + 9
Los valores de las variables o incógnitas (letras) que hacen que se
verifique la igualdad son lo que denominamos soluciones de
la ecuación. Así, en el ejemplo anterior, x=3 sería una
solución, ya que hace que se verifique la igualdad al sustituir x por 3:
7·3 – 3 = 3·3 +
9
21 – 3 = 9 + 9
18 = 18
ELEMENTOS DE
UNA ECUACIÓN
Los miembros de una ecuación son cada una de las
expresiones que aparecen a ambos lados del signo igual.
Los
términos son
los sumandos que forman los miembros.
Las incógnitas son las letras que aparecen en la ecuación.
Las
soluciones son los valores que deben tomar las letras para
que la igualdad sea cierta.
El grado de una ecuación es el mayor de los grados de
los monomios que forman sus miembros.
RESOLVER
ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA
Para resolver ecuaciones
lineales con una incógnita, deben ejecutarse algunos pasos:
1. Agrupar
los términos con X hacia el primer miembro y los que no llevan X al segundo miembro. Es
importante recordar que cuando un término pasa al otro lado de la igualdad, su
signo cambia (si es positivo pasa a ser negativo y viceversa).
3. Se
realizan las operaciones
respectivas en cada miembro de la ecuación. En este caso, corresponde
una suma en uno de los miembros y una resta en el otro, lo que da como
resultado:
4. Se
despeja la X, pasando
el término que tiene adelante al otro lado de la ecuación, con signo opuesto.
En este caso, el término está multiplicando, así que ahora pasa a dividir.
5. Se
resuelve la operación para
conocer el valor de X.
Entonces, la resolución de la
ecuación de primer grado quedaría de la siguiente manera:


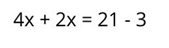

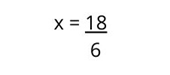


No hay comentarios:
Publicar un comentario